1) أي نقطتين في الفراغ يمر بهما مستقيم واحد فقط.
2) يتعين المستوى بثلاث نقاط ليست على استقامة واحدة أو مستقيمان متقاطعان أو مستقيم ونقطة خارجة عنه أو مستقيمين متوازيين.
3) المستوى يحوي ثلاث نقط على الأقل ليست على استقامة واحدة
4 ) المستوى هو ذلك السطح الذي إذا اختيرت نقطتان عليه فالمستقيم المار بهما يقع بأكمله في المستوى (منطق على ذلك السطح).
5) إذا اشترك مستقيم ومستوى في نقطتين فالمستقيم يقع بكامله في المستوى.
6) يتقاطع المستويان في مستقيم يعرف بخط تقاطعهما المشترك.
7) إذا اشترك مستويان في نقطة وفلا بد أن تقع على خط تقاطعهما ولا بد من أنهما متقطعان..
8) من نقطة خارج مستقيم لا يمكن رسم إلا مستقيم واحد يوازي المستقيم المفروض
9) المستقيمان اللذان لا يلتقيا أما أن يكونا متوازيين إذا جمعهما مستوى واحد وإلا فإنهما متخالفان
10) تقاس الزاوية بين المستقيمين المتخالفين برسم مستقيم يوازي أحدهما من نقطة على الآخر (أتفق على الزاوية الحادة)ز
11) إذا اشترك مستويان في ثلاث نقط ليست على استقامة واحدة فإنهما منطبقان.
12) المستقيم ل يوازي المستوى ى أي لا يلتقيا أو ل منطبق على ى.
13) إن لم يكن ل // س فإنه يقطعه في نقطة ب مثلاً.
14) يتوازى المستويان إذا اشتركا في ثلاث نقط (منطبقان) أو لا يلتقيا مهما امتدا .
15) إذا وازى مستقيم ل خارج المستوى ى مستقيماً في المستوى س فإن ل // ى.
16) إذا وازى مستقيم ل مستوى ى فكل مستوى يمر بالمستقيم ل يقطع المستوى ى في مستقيم ك فإن ل // ك.
17) إذا قطع مستوى مستويان متوازيان فإن خطا تقاطعه معهما متوازيان.
18) المستقيم العمودي على مستقيمين في مستوى واحد يكون عمودي على مستويهما أو عمودي على مستقيمين عند نقطة تقاطعهما.
19) المستقيمان العمودان على مستوى واحد متوازيان.
20) المستقيمان المتوازيان إذا كان أحدهما عمودي على مستوى فالآخر عمودي عليه.
21) إذا توازى مستقيمان فالمستوى المار بأحدهما يكون موازياً الآخر
22) إذا قطعت ثلاثة مستويات متوازية بمستقيمين فإن أطوال القطع المستقيمة المحصورة بينهما تكون متناسبة.
23) المستقيمان الموازيان لثالث في الفراغ متوازيان.
24) إذا مر مستويان بمستقيمين متوازيين فإن خط تقاطع المستويان يوازي كلاً من المستقيمين المتوازيين.
25) إذا وازى مستقيمان متقاطعان مستقيمان آخران متقاطعان فالزاوية بين المستقيمين الأوليين مساوية للزاوية بين الآخرين أو مكملة لها.
26) إذا كان مستقيماً عمودي على مستوى فكل مستوى يمر بهذا المستقيم يكون عمودياً على المستوى.
27) إذا تعامد مستويان ووجد مستقيم في أحدهما عمودي على خط تقاطعهما فإنه يكون عمودي على المستوى الآخر.
28) المستويان المتقاطعان وعمدان على مستوى ثالث فإن خط تقاطعهما يكون عمودي على المستوى الثالث.
29) تعرف الزاوية بين مستويين بالزاوية الزوجية بينهما وتقاس بالزاوية المحصورة بين العمودين المقامين من نقطة على خط تقاطعهما.
30) إذا كانت الزاوية الثنائية بين مستويين قائمة كان المستويان متعامدين، والعكس صحيح.
31) المستقيم ل المائل على المستوى ى والعمودي على المستقيم ك في ى فإن مسقط ل على س يكون عمودي على ك.
32) إذا كان المستقيم ل المائل على المستوى ى مسقطه عمودي على مستقيم ك في ى فإن ل يكون عمودي على ك.
حجم الموشور = مساحة قاعدته × الارتفاع
المساحة الجانبية الموشور المائل = محيط القاعدة × ارتفاعه الجانبي
المساحة الجانبية الموشور القائم = محيط القاعدة × ارتفاعه (طول حرفه الجانبي)
المساحة الكلية = المساحة الجانبية + مساحة القاعدتين
متوازي السطوح:
موشور قاعدته متوازي أضلاع. (جميع أوجهه الجانبية متوازيات أضلاع)
أقطاره تتقاطع في نقطة واحدة منتصف كل منها
متوازي المستطيلات:
منشور رباعي قائم قاعدته مستطيل وبالتالي جميع أوجهه مستطيلات.
أقطاره متساوية ومربع أي منها يساوي مجموع مربعات ثلاث أحرف منه متلاقية في نقطة واحدة.
حجم متوازي المستطيلات = الطول × العرض × الارتفاع أو مساحة القاعدة × الارتفاع
يمكن اعتبار أي وجه في كل من متوازي السطوح أو متوازي المستطيلات قاعدة لمنشور رباعي.
المكعب: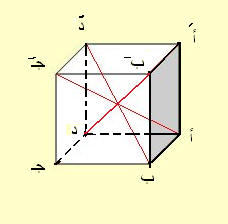
متوازي مستطيلات جميع أحرفه متساوية.
مربع قطره يساوي 3 أمثال مربع طول ضلعه
حجم المكعب = ل3 حيث ل طول حرفه
المساحة الجانبية للمكعب = 4 ل2
المساحة الكلية للمكعب = 4 ل2 + 2 ل2 = 6 ل2 ( 2 ل2 مساحة القاعدتين)
الزاوية بين وجه في الم و شور وقاعدته:
هي الزاوية الثنائية (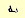
) بين أحد الأوجه والقاعدة والمبينة بالشكل
حيث: ع ارتفاع الموشور.
ع ـ ارتفاعه الجانبي.
الموشور المائل يكافئ الموشور القائم الذي قاعدته المقطع القائم للموشور المائل وارتفاعه يساوي الحرف الجانبي في الموشور المائل
*****
يمكن أن نقول الاسطوانة هي منشور قاعدتيه دائرتان
وتتولد الاسطوانة الدائرية القائمة أيضاً من دوران مستطيل حول أحد بعديه دورة كاملة ويكون هذا البعد ارتفاع الاسطوانة (ع) والبعد الآخر نصف قطرها (نق).
وتتولد الاسطوانة عن حركة مستقيم مواز لنفسه قاطعاً محيط دائرة ويعرف هذا المستقيم براسم الاسطوانة.
يسمى البعد بين مركزي قاعدتي الاسطوانة(دائرتان) محور الاسطوانة.
إذا لم تكن قاعدتا الاسطوانة متوازيتان كانت الاسطوانة ناقصة، وذكر كلمة اسطوانة يعني اسطوانة دائرية قائمة تامة (كاملة).
حجم الاسطوانة:
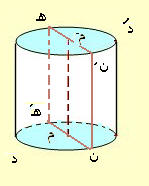
حجم الاسطوانة = مساحة القاعدة × الارتفاع ( هي حالة خاصة من المنشور)
المساحة الجانبية للاسطوانة = محيط القاعدة × الارتفاع
=2 ╥ نق × ع
= 2 ╥نق ع
المساحة الكلية للاسطوانة = المساحة الجانبية + مساحة القاعدتين
= 2 ╥ نق ع + 2 ╥ نق2 ( مساحة الدائرة =╥ نق2 )
= 2 ╥ نق( ع + نق)
إذا تساوى حجما اسطوانتين دائرتين قائمتين كانت النسبة بين مساحتيهما تساوي النسبة العكسية لنصفى قطري قاعدتيهما.
إذا تساوت المساحتان الجانبيتان لأسطوانتين دائرتين قائمتين كانت النسبة بين حجميهما كالنسبة بين نصفى قطري قاعدتيهما.
***
قاعدة الهرم هي ذلك المضلع والرأس المشترك للمثلثات هو رأس الهرم والمثلثات هي أوجه الهرم الجانبية والعمود النازل من رأس الهرم على قاعدته هو ارتفاع الهرم ويسمى الهرم حسب عدد أضلاع قاعدته فإن كانت مثلث قيل هرم ثلاثيويسمى الهرم قائم إذا كان موقع العمود من الرأس على القاعدة وهي مضلع منتظم هو مركز القاعدة (المضلع المنتظم ما كانت أضلاعه وزواياه متساوية كالمثلث المتساوي الأضلاع).
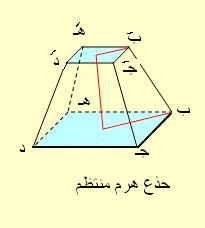
إذا قطع الهرم بمستوى يوازي قاعدته نشأ هرم ناقص متوازي القاعدتين النسبة بين مساحتي القاعدتين كالنسبة بين مربعي بعديهما عن رأس الهرم.
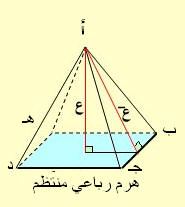
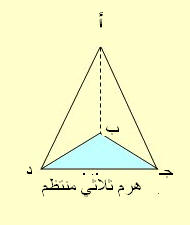
حجم الهرم = ـــ مساحة القاعدة × الارتفاع
3
المساحة الجانبية للهرم = نصف محيط قاعدته × عامد
المساحة الكلية للهرم = المساحة الجانبية + مساحة قاعدته
1 ــــــــــــــــ
3
المساحة الجانبية لجذع الهرم = نصف مجموع محيطي قاعدتيه × عامد
المساحة الكلية لجذع الهرم = المساحة الجانبية + مساحتي قاعدتيه
المخروط
كما ينشأ المخروط الناقص الدائري القائم من دوران شبه منحرف قائم حول ارتفاعه دورة كاملة.
كما يتولد المخروط الدائري القائم من دوران مثلث قائم حوا أحد ضلعي القائمة.
1
حجم المخروط الدائري القائم = ـــ مساحة القاعدة × الارتفاع
3
1
حجم المخروط الدائري القائم = ـــ╥ نق 2× ع
3
1
حجم المخروط الدائري القائم = ـــ╥ ع 3 طا 2هـ حيث هـ الزاوية نصف الرأسية
3
1
حجم المخروط الدائري القائم = ـــ╥ نق 3 طتاهـ
3
1
ح جم المخروط الدائري القائم الناقص = ـــ ╥ ع [ (نق1)2 + نق1 نق2 + (نق2)2 ]
3
المساحة الجانبية للمخروط الدائري القائم = نصف محيط قاعدته × طول راسمه
= ╥ نق ل حيث ل طول راسم المخروط
ــــــــــــــــــــ
= ╥ نق / نق2 + ع2
المساحة الجانبية لجذع المخروط = نصف مجموع محيطي قاعدتيه المتوازيتين × طول حرفه
= ╥ ( نق1 + نق2) × ح
المساحة الكلية = المساحة الجانبية + مساحة القاعدة للمخروط الدائري القائم
المساحة الكلية = المساحة الجانبية + مساحة القاعدتين لجذع المخروط
الكـرة
تسمى النقطة الثابتة بمركز الكرة والبعد الثابت بنصف قطر الكرة (نق).
وتنشأ الكرة من دوران نصف دائرة دورة كاملة حول قطرها.
المقطع الحادث من قطع الكرة بمستوى يمر بمركزها هو دائرة نصف قطرها يساوي نصف قطر الكرة
، تسمى هذه الدائرة بالدائرة العظمى ويسمى المستوى بالمستوى المركزي أو القطري
إذا قطع كرة مستوى فالمستوى الحادث محيط دائرة صغرى ( المستوى لا يمر بالمركز)
4
حجم الكرة = ـــــ ط نق3
3
مساحة سطح الكرة = 4 ط نق2
يسمى السطح الكروي للكرة الناقصة بالمنطقة الكروية.
القطعة الكروية : إذا قطعت الكرة بمستو غير مار بالمركز انقسمت إلى جزأين يسمى كل منهما قطعة كروية ويكون المقطع قاعدة القطعة الكروية والعمود المقام من مركز المقطع (دائرة) ملاقي محيط الكرة في نقطة هو ارتفاع القطعة الكروية ( ن هـ في الشكل ).
يسمى السطح الكروي للقطعة الكروية بالطاقية الكروية، وهي حالة خاصة من المنطقة باعتبار أحد قاعدتيها مماس للكرة.
مساحة المنطقة الكروية = 2 ╥ نق ع حيث نق نصف قطر الكرة ، ع ارتفاع المنطقة الكروية.
مساحة الطاقية الكروية = 2╥ نق ع حيث نق نصف قطر الكرة ، ع ارتفاع القطعة الكروية.
╥ ع
حجــم المنطقة الكروية = ـــــــــ [ 3{(نق 1) 2 +(نق 2) 2 } + ع 2] ………… (1)
6
بوضع نق 2 = صفر في (1) فإن المنطقة الكروية تؤول إلى قطعة كروية نصف قطر قاعدتها نق 1 وارتفاعها ع فإن :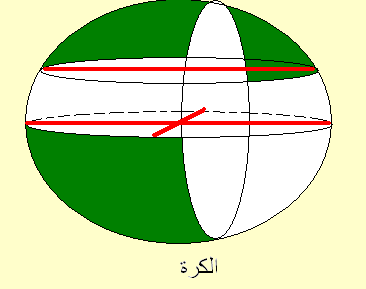
╥ ع
حجــم القطعـة الكروية = ــــــــــ [ 3 (نق1)2 + ع2]
6
بوضع نق 2 = 0 ، نق 1 = نق في (1) فإن ع تؤول إلى نق والمنطقة الكروية تؤول إلى نصف كرة نصف قطرها نق ومنها:
ط نق 2
حجــم نصـف الكـرة = ــــــــــ [ 3 نق 2 +نق 2] = ـــــ ط نق 3
6 3
2
حجــم نصـف الكـرة = ـــــ ╥ نق3
3
بوضع في (1) نق 2 = 0 ، نق 1 = 0 ، ع = 2نق فإن المنطقة الكروية تؤول إلى كرة نصف قطرها نق ومنها:
╥ × 2نق
6
4
حجــم الكـرة = ـــــ╥ نق3
3
