التدفق المغناطيسي Φ الذي يعبر سطح هو عدد خطوط الحقول المغناطيسي
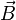والتي تعبر السطح 
و يعبر عنه بالجداء السلمي لشعاع الحقل المغناطيسي 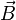و شعاع السطح
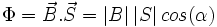واحده التدفق المغناطيسي هي الويبر Weber تكريما للفيزيائي الالماني ويليم ويبر [1804-1891] Wilhelm Eduard Weber
التدفق المغناطيسي عبارة عن قياس للمغناطيسية مع أخذ قوة و شدة الحقل المغناطيسي بالحسبان
فيما يلي نص بالانجليزيه
اذا اردت الرابط كاملا ادخل الى
http://en.wikipedia.org/wiki/Flux#Fl…and_theorems_2
Electromagnetism
[] Flux definition and theorems
An example of the second definition of flux is the magnitude of a river’s current, that is, the amount of water that flows through a cross-section of the river each second. The amount of sunlight that lands on a patch of ground each second is also a kind of flux.
To better understand the concept of flux in Electromagnetism, imagine a butterfly net. The amount of air moving through the net at any given instant in time is the flux. If the wind speed is high, then the flux through the net is large. If the net is made bigger, then the flux would be larger even though the wind speed is the same. For the most air to move through the net, the opening of the net must be facing the direction the wind is blowing. If the net opening is parallel to the wind, then no wind will be moving through the net. (These examples are not very good because they rely on a transport process and as stated in the introduction, transport flux is defined differently than E M flux.) Perhaps the best way to think of flux abstractly is “How much stuff goes through your thing”, where the stuff is a field and the thing is the imaginary surface.
The flux visualized. The rings show the surface boundaries. The red arrows stand for the flow of charges, fluid particles, subatomic particles, photons, etc. The ****** of arrows that pass through each ring is the flux.
As a mathematical concept, flux is represented by the surface integral of a vector field,
where
E is a vector field of Electric Force, dA is the vector area of the surface S, directed as the surface normal, Φ f is the resulting flux.The surface has to be orientable, i.e. two sides can be distinguished: the surface does not fold back onto itself. Also, the surface has to be actually oriented, i.e. we use a convention as to flowing which way is counted positive; flowing backward is then counted negative.
The surface normal is directed accordingly, usually by the right-hand rule.
Conversely, one can consider the flux the more fundamental quantity and call the vector field the flux density.
Often a vector field is drawn by curves (field lines) following the “flow”; the magnitude of the vector field is then the line density, and the flux through a surface is the ****** of lines. Lines originate from areas of positivedivergence (sources) and end at areas of negative divergence (sinks).
See also the image at right: the ****** of red arrows passing through a unit area is the flux density, the curveencircling the red arrows denotes the boundary of the surface, and the orientation of the arrows with respect to the surface denotes the sign of the inner product of the vector field with the surface normals.
If the surface encloses a 3D region, usually the surface is oriented such that the outflux is counted positive; the opposite is the influx.
The divergence theorem states that the net outflux through a closed surface, in other words the net outflux from a 3D region, is found by adding the local net outflow from each point in the region (which is expressed by thedivergence).
If the surface is not closed, it has an oriented curve as boundary. Stokes theorem states that the flux of the curlof a vector field is the line integral of the vector field over this boundary. This path integral is also calledcirculation, especially in fluid dynamics. Thus the curl is the circulation density.
We can apply the flux and these theorems to many disciplines in which we see currents, forces, etc., applied through areas.
[edit] Maxwell’s equations
The flux of electric and magnetic field lines is frequently discussed in electrostatics. This is because in Maxwell’s equations in integral form involve integrals like above for electric and magnetic fields.
For instance, Gauss’s law states that the flux of the electric field out of a closed surface is proportional to theelectric charge enclosed in the surface (regardless of how that charge is distributed). The constant of proportionality is the reciprocal of the permittivity of free space.
Its integral form is:
where
is the electric field, is the area of a differential square on the surface A with an outward facing surface normaldefining its direction, is the charge enclosed by the surface, is the permittivity of free space is the integral over the surface A.Either or is called the electric flux.
Faraday’s law of induction in integral form is:
The magnetic field is denoted by . Its flux is called the magnetic flux. The time-rate of change of the magnetic flux through a loop of wire is minus the electromotive force created in that wire. The direction is such that if current is allowed to pass through the wire, the electromotive force will cause a current which “opposes” the change in magnetic field by itself producing a magnetic field opposite to the change. This is the basis forinductors and many electric generators.
[edit] Poynting vector
The flux of the Poynting vector through a surface is the electromagnetic power, or energy per unit time, passing through that surface. This is commonly used in analysis of electromagnetic radiation, but has application to other electromagnetic systems as well.
