المحاضرات ل د/ الصادق معا فى صورة pdf:
http://www.herosh.com/download/20796…_____.pdf.html
بصورة عامة حل معادلة انشتاين يعطى الممتدد المترى و هو تلك الدالة التى تعرف طول الفترة فى الزمنكان
احتمالان:
1) اذا كان الممتدد المترى دالة ثابتة لا تعتمد على متغيرات الزمنكان (t, x,y,z) فان الفضاء يكون مستويا ولا يوجد به انحناء وعليه لا توجد جاذبية و تؤول النظرية النسبية العامة الى النسبية الخاصة
2) اذا كان الممتدد المترى دالة فى متغيرات الزمنكان فان الفضاء يكون منحنيا و توجد قوى جذب كونى
الان ماهو الممتدد المترى ؟
يعرف الممتدد المترى على انه يعطى تعريفا لطول المتجة فى الفضاء
دعنا نبدأ من فيثاغورث و افترض متجهين يعطيان ب
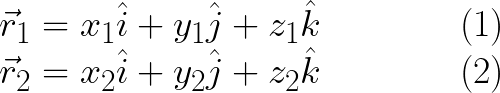
ماهو البعد بين هذين المتجهين؟ بالطبع البعد هو القيمة المطلقة للفرق بين المتجهين
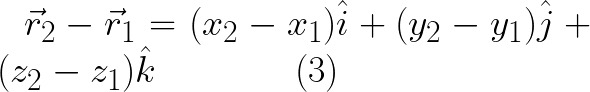
ولما كان المتجين قريبين من بعضهما البعض فان الفرق فى الاحداثيات يمكن تمثيله كتغير طفيف يعبر عنه بالرمز dr وعليه نعيد كتابة المعادلة (3) على النحو المختصر التالى :
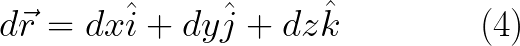
وهكذا نجد ان مربع طول المتجة يعطى بالضرب القياسى للمتجه dr مضروبا فى نفسه (فيثاغورث فى ثلاثة ابعاد x ,y,z) اى ان
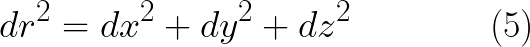
الان نريد كتابة هذه المعادلة على النحو الذى يسمح بتعريف الممتدد المترى
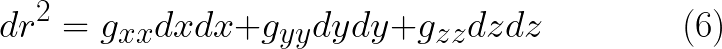
حيث ان المعاملات التى تظهر فى مقدمة مربع التغير فى x و y و z تساوى الواحد الصحيح فى هذا المثال لاننا نتحدث عن بعد بين متجهين فى فضاء مستوى ولكن بشكل عام فى الفضاءت غير المستوية تكون هذه المعاملات دوال فى x و y و z وهذه المعاملات تعرف على انها مركبات الممتدد المترى
الممتد المترى فى فضاء مستوى رباعى الابعاد
تعلمنا من النظرية النسبية الخاصة بان الزمن يعامل على انه بعد رابع وعليه يصبح الفضاء زمنكانيا بدلا عن مكانيا ويكون المتجه فى الزمنكان متجه رباعى الابعاد
الطول الفاصل بين اى متجهين رباعيين يحمل خاصية المكان و خاصية الزمان ونسميه بالفترة المكانية-الزمانية (الفترة الزمنكانية) ويرمز لطول الفترة بالرمز ds
الان نستطيع تكرر نفس الخطوات فى حساب مربع طول متجه فى فضاء ثلاثى الابعاد من اجل حساب مربع طول الفترة الزمنكانية, وببساطة سوف نقوم باضافة مربع البعد الزمنى للمعادلة (5) ولكن كم تعلم ان البعد الزمنى فى النسبية الخاصة هو بعد تخيلى ict ولهذا فان مربعه يكون سالبا
وعليه يكون
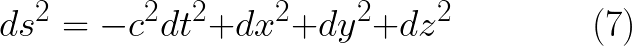
والتى يمكن اعادة كتابتها على نفس النحو الذى اتخذناه فى كتابة المعادلة (6) لنحصل على
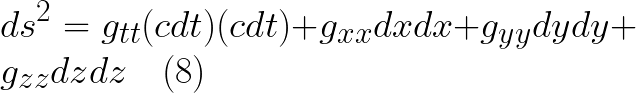
حيث المعامل 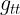 يساوى -1 و بقية المعاملات تساوب +1 فى هذا المثال لفضاء مستوى رباعى الابعاد اما بشكل عام فان هذه المعاملات تكون دوال فى متغيرات الزمنكان وتظل دائما المركبة الزمانية للممتدد المترى دالة سالبة الاشارة بينما بقية المركبات تكون دوال موجبة الاشارة
يساوى -1 و بقية المعاملات تساوب +1 فى هذا المثال لفضاء مستوى رباعى الابعاد اما بشكل عام فان هذه المعاملات تكون دوال فى متغيرات الزمنكان وتظل دائما المركبة الزمانية للممتدد المترى دالة سالبة الاشارة بينما بقية المركبات تكون دوال موجبة الاشارة
ترميز
من اجل الاختصار سوف نقوم بتغير الترميز وذلك لكى نختصر الكتابة
سوف نسمى البعد الزمنى بالبعد الصفرى و البعد فى x بالبعد الاول والبعد فى y بالبعد الثانى والبعد فى z بالبعد الثالث ونعبر عن كل هذا بالشكل المختصر التالى :
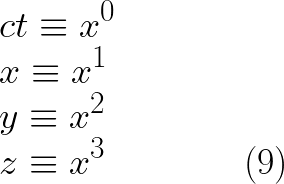
لاحظ ان المعامل اعلى x لا يمثل اسا وانما فقط رقم يمثل ترتيب البعد
واذا قمنا باستبدال الترميز القديم بهذا الترميز (فقط استبدل ct و x و y و z بمقابلاتها فى المعادلة (9)) فى معادلة مربع الفترة (8) نحصل على الشكل التالى :
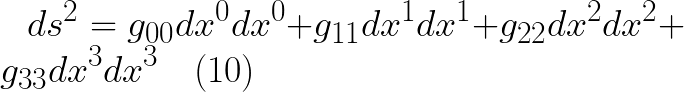
المركبات 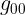 و
و 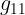 و
و 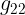 و
و 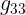 تمثل مركبات الممتدد المترى فى الفضاء الزمنكانى المستوى رباعى الابعد واذا كانت هذه المركبات تعتمد المتغيرات الزمنكانية فان تكون ملركبات الممتدد المترى للزمنكان المنحنى رباعى الابعاد
تمثل مركبات الممتدد المترى فى الفضاء الزمنكانى المستوى رباعى الابعد واذا كانت هذه المركبات تعتمد المتغيرات الزمنكانية فان تكون ملركبات الممتدد المترى للزمنكان المنحنى رباعى الابعاد
نوعان من المتجهات الرباعية
نعلم من مبادئ الجبر الخطى ان المتجه يمكن تمثيله بمصوفة عمودية (بها عمود واحد وعدة صفوف) او بمصفوفة صفية (بها صف واحد وعدة اعمدة)
الان دعنا نمثل المتجه الرباعى على النحو التالى
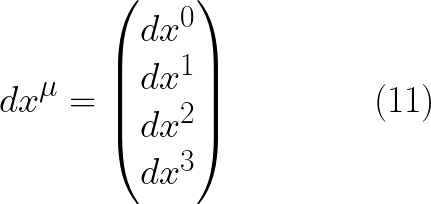
حيث المعامل ميو يأخذ القيم 0و 1 و 2 و 3 وبالطبع اذا اخذ ميو القيمة 0 فان هذا يقابل الصف الصفرى و اذا اخذ ميو القيمة 1 فهذا يقابل الصف 1 …الخ
لاحظ اننا لكى نضرب اى مصفوفتين فيجب ان يكون عدد اعمدة المصفوفة الا ولى مساوى لعدد صفوف المصفوفة الثانية و فبما عدا هذا فان ضرب المصفوفة الاولى فى الثانية لن يكون معرفا (ممكننا). ولهذا السبب سوف نحتاح الى تحويل المتجه الرباعى من مصفوفة عمودية الى مصفوفة صفية لكى نتمكن من ضربه فى نفسه لكى نحصل على مربع طول المتجه الرباعى .
ولكى نمييز بين المتجه الرباعى الممثل بمصفوفة عمودية و المتجه الرباعى الممثل بمصفوفة صفية سوف نكتب المعامل ميو اعلى x فى حالة المصفوفة العمودية ونكتبه اسفل x فى حالة المصفوفة الصفية اى ان
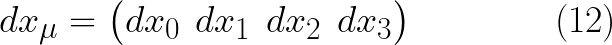
الان نريد استخدم مفهوم ضرب مصفوفتين فى تعريف مربع الفترة ودعنا فقط نضرب المصفوفة الصفية للمتجه الرباعى فى المصفوفة العمودية لحصل على المعادلة التالية
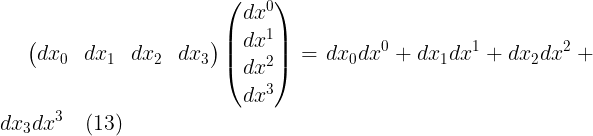
وبمقارنة سريعة بين هذه المعادالة والمعادلة (10) نجد ان :
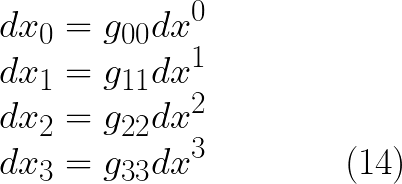
اى ان مركبات الممتدد المترى تعمل على تنزيل المعامل من اعلى x الى اسفل x . من الان ولاحقا سوف نسمى المتجه الرباعى الذى يمثل بمصوفة عمودية (ميو توجد فى اعلى x ) بمتجه كونترافيرينت contravariant اما المتجه الرباعى الذى يمثل بمصفوفة صفية (ميو توجد فى اسفل x) بمتجه كوفيرينت covariant
وهكذا يعمل الممتدد المترى على تحويل الكونترافيرينت الى كوفيرينت (والعكس ايضا صحيح)
تمثيل الممتدد المترى
المعادلة (14) يمكن كتابتها بالصورة المصفوفية التالية
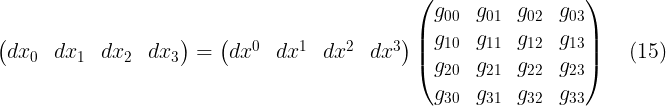
حيث ان جميع العناصر التى لا تقع فى القطر الرئسى (عندما يختلف رغم الصف عن رغم العمود ) مساوىة للصفر بالنسبة لمثالنا فى الفضاء المستوى رباعى الابعاد ولكن فى الحالة العامة قد لا تساوى جميعها الصفر. وهذه المعادلة توضح كيفية تحويل الكونترافيرينت الى كوفيرينت, والان بتعويض المتجه الكوفيرينت من المعادلة (15) فى المعادلة (13) نحصل على مربع طول الفترة بالصورة المصفوفية التالية
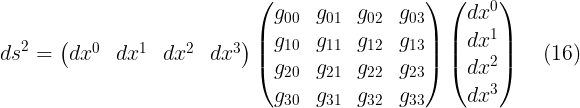
نلاحظ من هذه المعادلة ان الممتدد المترى عبارة عن مصفوفة مربعة من النظام 4 فى 4 اى ان بها اربعة صفوف واربعة اعمدة وهذه المصفوفة يعبر عنها بالصورة المختصرة التالية :

وهى تمثل ممتدد مترى من الرتبة الثانية ومن النوع كوفيرينت وذلك لان المعاملات ميو (رغم الصف) و نيو (رغم العمود) موجودة فى اسفل g
وهى عبارة عن مصفوفة غير شاذه بمعنى انها قابلة للعكس ومعكوسها الضربى هو ايضا مصفوفة مربعة وتسمى بالممتدد المترى من الرتبة 2 ومن النوع كونترافيرينت (لان المعاملات ميو و نيو توجد فى اعلى g) ويعبر عنها بالصورة التالية:
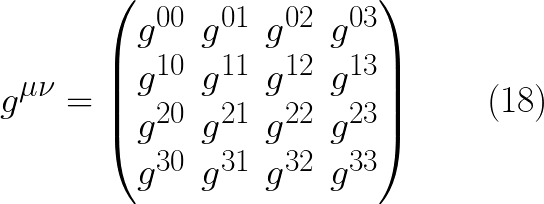
ومثلما كان الممتدد المترى من النوع كوفيرينت يحول المتجه الرباعى كونترافيرينت الى كوفيرينت فان الممتدد المترى من النوع كونترافيرينت يحول المتجه الرباعى كوفيرينت الى كونترافيرينت
قاعدة تجميع انشتاين
الان سوف افترض ان القارئ ملم بمبادئ جبر المصفوفات ويستطيع ايجاد حاصل الضرب للمصفوفات فى المعادلة (16) وسوف نحصل على النتيجة التالية بعد اجراء عملية الضرب المباشرة
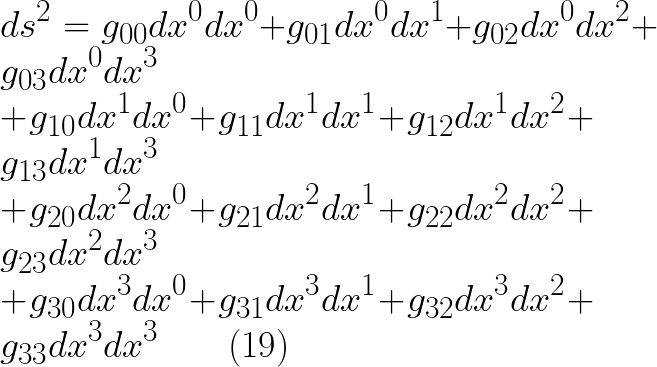
لاحظ تكرار 0 فى رغم الصف فى g وفى dx الاةلى فى جميع الحدود فى السطر الاول من المعادلة الاخيرة وهكذا نستطيع كتابة السطر الاول فى شكل مجموع بالصورة التالية:
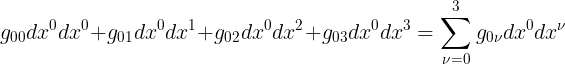
اما فى السطر الثانى فيتكرر المعامل 1 وهكذا نستطيع كتابته بالمجموع التالى
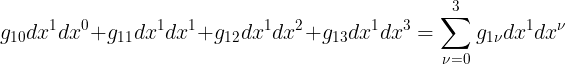
اما فى السطر الثالث فان المعامل المتكرر هو 2 لذا نجد ان :
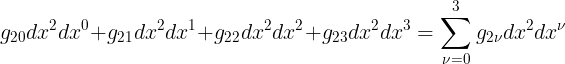
واخيرا يتكرر المعامل 3 فى السطر الرابع وعليه يكون
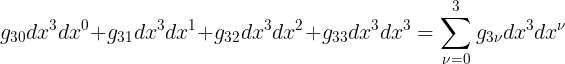
الان عوض المجاميع هذه فى المعادلة (19) لتحصل على مربع الفترة التالى
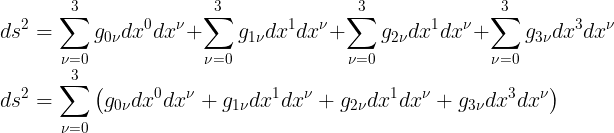
لاحظ تكرر المعامل نيو فى رغم العمود فى g وفى dx الثانية فى جميع حدود المعادلة الاخيرة وهكذا وبنفس الطريقة السابقة نستطيع كتابة تجميع جديد
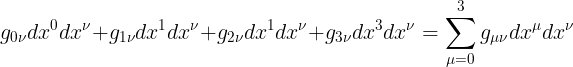
عوض هذا التجميع فى المعادلة الاخيرة لتحصل على الصورة التالية لمربع طول الفترة
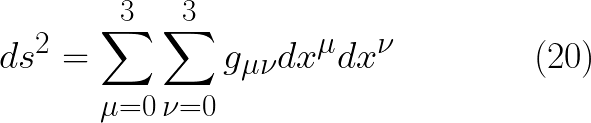
قاعدة جمع انشتاين هى اصطلاح اسقاط رمز التجميع عند تكرر معامل مرة فى الاسفل فى حد ومرة فى الاعلى فى حد ثانى لذا نسقط رمز التجميع على ميو لظهورها فى الاسفل فى g وفى الاعلى فى dx الاولى و ايضا نسقط رمز التجميع على نيو نسبة لظهورها فى اسفل g وفى اعلى dx الثانية
لاحظ اننا نسقط رمز التجميع فقط من اجل اختصار الكتابة ولكن لا نسقط عملية التجميع نفسها اى ان تكرار المعامل دليل على عملية تجميع
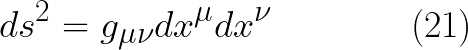
والان اذا رفعت معامل فى احد الحدود فيجب تنزيل هذا المعامل فى الحد الاخر اى مثلا نجد ميو فى اسفل g وفى الاعلى فى dx فتستطيع رفع ميو فى اعلى g بشرط تنزيله فى اسفل dx ونفس الامر يمكن تطبيقه على نيو لنحصل على
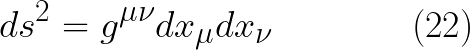
لماذا نسبية عامة؟
ماهو السبب الذى جعل انشتاين يضع نظريته للنسبية العامة؟ أو بمعنى اخر ما عيب الوصف النيوتونى للتثاقل الكونى حتى يتم استبداله بنظرية النسبية العامة؟
عندما وضع انشتاين نظرية النسبية الخاصة, الزم جميع القوانين الفيزيائية بان تكون لا متغيرة تحت تأثير تحويلات لورنتز, كما هو معلوم ان معادلة نيوتن للتثاقل الكونى (قانون الجذب العام) لا تحقق تحويلات لورنتز, وانها تتنبأ بتفاعل تجاذبى لحظى اى ان سرعة انتقال التفاعل التثاقلى لانهائية. دعنا نعطى مثال لذلك حتى لا يتوه القارئ بين التعبيرات العلمية الجامدة وحتى تتكون لديه صورة ذهنية لتقريب الصورة الفيزيائية
تترتبط الارض مع الشمس بقوى جذب تثاقلى تجعل الارض تدور حول الشمس, ولكن اذا افترضنا ان الشمس لسبب ما قد اختفت فجاءة!!!! ماذا يحدث للارض؟ بالطبع حسب نظرية نيوتن لا توجد سرعة قصوى فى الطبيعة لذلك نجد ان المجال التثاقلى الذى ينتقل بين الشمس والارض يتحرك بسرعة لانهائية وعليه يقطع المسافة بينهما فى فى زمن يساوى الصفر وهكذا اذا اختفت الشمس سوف يتوقف المجال التثاقلى وتتوقف الارض عن الدوران فى نفس لحظة اختفاء الشمس.
والان مالذى جعل انشتاين غير سعيدا بهذه النتيجة؟ حسب مفاهيم النسبية الخاصة توجد سرعة القصوى لانتقال التفاعل وهذه السرعة القصوى هى سرعة الضوء. واذا افترضنا ان الشمس قد اختفت فجاءة بعد ارسالها للمجال التثاقلى, فان المجال سوف يتحرك باقصى سرعة ممكنة (سرعة الضوء) ليصل الى الارض بعد فترة زمنية تصل الى 8 دقائق تقريبا, وعليه لن تعرف الارض اختفاء الشمس الا بعد مرور 8 دقائق وسوف تظل تدور حول موقع الشمس المزعوم لمدة ثمانية دقائق قبل ان تكف عن الدوران.
وهكذا نجد ان نظرية نيوتن للتثاقل الكونى تتناقض مع فرضيات النسبية الخاصة لذا يجب تعديلها او استبدالها بنظرية اخرى تكون متوافقة مع النسبية الخاصة.
والان بعد ان عرفنا ان نظرية نيوتن للتثاقل الكونى لا يمكن ان تكون الكلمة النهائية لوصف القوى التثاقلية , نريد ان نعرف كيفية ايجاد نظرية بديلة لها. مدخل انشتاين لايجاد هذه النظرية يتمحور حول ثلاثة نقاط رئيسية وهى
(1) مبدأ التكافؤ فى النسبية الخاصة.
(2) العلاقة بين كتلة القصور وكتلة التثاقل
(3) النسبية الخاصة و التسارع.
النقطة الاولى:
كما هو معلوم ان النسبية الخاصة افترضت وجود مناطات اسنادية مفضلة لوصف القوانين الطبيعة وهذه المناطات تسمى بمناطات القصور وهى المناطات التى تتحرك بالنسبة لبعضها البعض بسرعات منتظمة (ثابتة) وفى خط مستقيم . ولكن دعنا الان نطرح السؤال التالى ونترك الاجابه عليه لفطنة القارئ , مالذى يميز السرعات الثابتة عن غيرها؟ لماذا تكون السرعات الثابتة مفضلة؟ او على بصورة اعمق, سرعات ثابتة بالنسبة لماذا؟ هل بالنسبة لفضاء مطلق؟ ام بالنسبة لنجم ثابت؟ …الخ؟
النقطة الثانية:
فى الميكانيكا النيوتونية يوجد مفهومين مستقلين للكتلة وهما كتلة القصور وهى التى تمانع التسارع وهى تجعل الجسم قاصرا عن الحركة مالم تؤثر عليه قوى خارجية تجعله يتسارع. وكتلة اخرى تعرف بكتلة التثاقل وهى الكتلة المرتبطة بقوى التثاقل. الان يوجد تأكيد عملى غير قابل للشك ينص على ان الكتلتين متساويتين, بمعنى ان جميع الاجسام تسقط بنفس المعدل فى وجود حقل تثاقلى, او بصورة اخرى ان كتلة القصور التى تقوم تسارع الجسم تساوى كتلة الثاقل التى جعلت الجسم يتفاعل مع الحقل التاقلى.
ولما كانت نظرية نيوتن تفضل ان تكون كتلة القصور مختلفة عن كتلة التثاقل, وكانت الحقائق التجريبية تنص على تساوى الكتلتين. اعتبر انشتاين ان عملية تساوى الكتلتين هذا ربما يقود الى المعنى العميق لطبيعة قوى التثاقل, وبحنكة وعبقرية استطاع انشتاين من هذه الملاحظة البسيطة ان تساوى كتلة القصور مع كتلة التثاقل يوحى بعلاقة بين القصور (التسارع) وقوى التثاقل نفسها و قال:
محليا (فى حيز صغير- سوف نرجع لهذه المفهوم لاحقا) لا نستطيع التمييز بين قوى التثاقل والتسارع
محليا: التثاقل=القصور=التسارع
مبدأ التكافؤ فى النسبية
دعنا نتخيل صندوق مغلق تماما (مصعد) موضوع فى مكان ما فى الفراغ الخارجى و بداخل هذا المصعد مراقب. افترض عدم وجود اى نوع من انواع تؤثر على المصعد و لذلك فان المراقب سوف يسبح بحرية تامة (لانعدام الوزن) داخل المصعد, اذا كان المراقب يحمل فى كلتا يديه كرتين وقام بتركهما فى لحظة ما ليسبحان معه داخل المصعد
افترض وجود شخص ما قام بربط المصعد من سقفه بسلسلة و سحبه الى اعلى بعجلة ثابته, وهكذا سوف يرتفع المصعد وترتفع مع ارضية المصعد لتصطدم بقدمى المراقب وبالكرتين وصديقنا داخل المراقب سوف يشعر بقوى تضغط على قدمية ويرى الكرتين وهما تسقطان نحو ارضية المصعد وهما يسلكان مساريين متوازيتين اثناء سقوطهما
انظر الى الشكل ادناه الى جهة اليسار

دعنا الان نفترض ان المصعد موضوع فى حقل تثاقلى كما هو مبين فى الرسم اعلاه فى جهة اليمين , سوف يشعر المراقب بقوى تضغط على قدميه وسوف يرى الكرتين وهما تسقطان نحو ارضية المصعد ولما كانت قوى الجذب تجذب الكرتين نحو مركز الكتلة المسببة للحقل التثاقلى فان الكرتان سوف تسقطان نحو حو الارضية سالكتين مساريين متقاربين, ولكن اذا كانت المسافة (وهى كذلك) بين الكرتين صغيرة جدا بالمقارنة مع نصف قطر مركز الكتلة التى انتجت قوى التثاقل (هذا هو مفهوم المحليه) فان المراقب لن يستطيع مشاهدة تقارب مسار الكلاتين , وعليه لا توجد اى تجربة يمكن للمراقب داخل المصعد ان يقوم باجراءها ليقرر ما اذا كان القوى المؤثرة على المصعد هى قوى تثاقل كونى تجذبه مع كرتيه الى اسفل ام ان هناك شخص خارج المصعد قام بسحبه الى اعلى بتسارع ثابت
وهكذا لا يمكن محليا التمييز بين التسارع و قوى التثاقل
تحويل الاحداثيات
الان سوف نوقف الحديث عن قوى التاقل الى حين, وسوف نتناول موضوع تحويل الاحداثيات حتى يتمكن القارئ من فهم الدور الذى يلعبه الممتدد المترى فى وصف منظومات الاحداثيات وليتعرف ايضا على التغير الذى يطراء على الممتدد المترى عند التحويل من اطار الى اخر .
دعنا نبدأ بمثال بسيط لمنظومة احداثيات مستوية فى فضاء ثنائ الابعاد, ولتكن المنظومة الكارتيزية x و y نريد ايجاد تحويل من الاحداثيات الكارتيزيه هذه الى نظام الاحداثيات القطبى (الدائرى) المعرف بنصف قطر r وزاوية 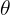

يتضح من الرسم اعلاه ان جيب تمام الزاوية 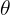 يساوى حاصل قسمة الضلع المجاور للزاوية x مقسوما على الوتر اما جيب الزاوية
يساوى حاصل قسمة الضلع المجاور للزاوية x مقسوما على الوتر اما جيب الزاوية 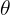 فيساوى حاصل قسمة الضلع المقابل للزاوية y مقسوما على الوتر
فيساوى حاصل قسمة الضلع المقابل للزاوية y مقسوما على الوتر
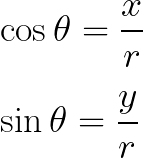
وبضرب الطرفين فى اى من المعادلتين فى r نحصل على معادلات التحويل من النظام الكارتيزى الى النظام القطبى الدائرى
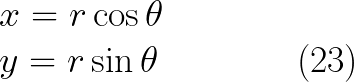
يمكن للقارئ ان يفهم المعادلات اعلاه على انها اسقاطات للمتجه r بحيث يكون الاسقاط المجاو للزاوية x يعطى بحاصل ضرب نصف القطر مضروبانا فى جيب تمام الزاوية, اما الاسقاط المقابل y يعطى بحاصل ضرب نصف القطر فى جيب الزاوية, هذه القاعدة سوف تكون مفيدة عند تناول عملية تحويل المحاور الكارتيزية x و y و z الى نظام الاحداثيات الكروية.
الان دعنا نحسب التغير فى المحاور x و y بدلالة التغيرات المقابلة فى نظام الاحداثيات الدائرى, من اجل هذه الحسابات يحتاج القارئ لمعرفة مبادئ التفاضل البسيطة, ولكى نعطى وصفا ذاتيا متكاملا لمادة هذا الموضوع سوف اضع علاقة عامة لتعريف التغير فى دالة ما
افترض دالة 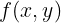 تعتمد على المتغيرات x و y. الان نجد ان التغير فى الدالة f يعطى بقاعدة السلسلة التالية
تعتمد على المتغيرات x و y. الان نجد ان التغير فى الدالة f يعطى بقاعدة السلسلة التالية
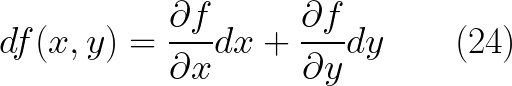
بالرجوع الى المعادلة (23) نجد ان x و y دوال فى كل من r و سيتا وعليه بتطبيق قاعدة السلسلة (24) نحصل على
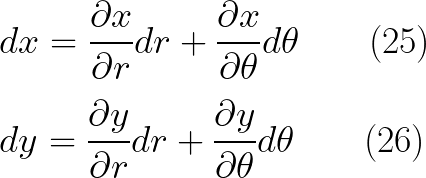
ومن المعادلات (23) يمكن حساب التفاضلات اعلاه
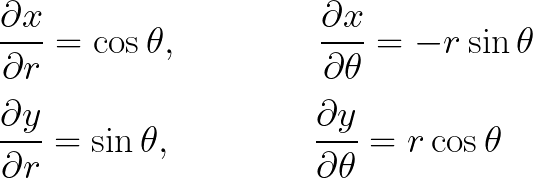
وبالتعويض المباشر فى المعادلات (26) نجد ان
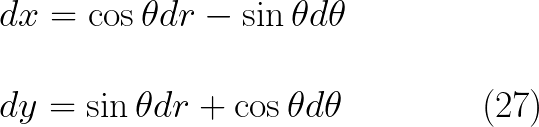
وهكذا نستطيع حساب مربع عنصر الطول فى الاحداثيات القطبية على النحو التالى
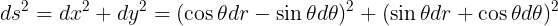
وبفك التربيع فى المعادلة اعلاه نحصل على
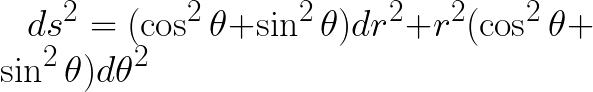
واستخدام العلاقة المثلثية 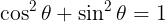 نحصل على
نحصل على
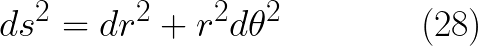
والتى يمكن اعادة كتابتها بالصورة التالية
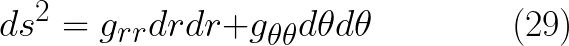
وبمقارنة المعالة (29) مع المعادلة (28) نحصل على قيم المعاملات والتى تمثل مركبات الممتد المترى فى نظام الاحداثيات الدائرية

وبقية المعاملات التى لم تظهر فى المعادلة (28) تساوى اصفارا يمكن ترتيب مركبات g فى شكل مصفوفة على النحو التالى :
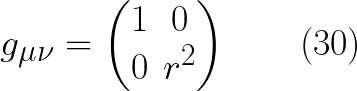
وهذا هو الممتد المترى فى نظام الاحداثيات الدائرى
دعنا الان نتحث عن منظومة احداثيات مستوية فى فضاء ثلاثى الابعاد, ولتكن المنظومة الكارتيزية x و y و z. والمطلوب هو ايجاد تحويل من الاحداثيات الكارتيزيه هذه الى نظام الكروية المعرفة بنصف قطر r وزوايا و
الان سوف نطبق قاعدة الاسقاط التى تحدثنا عنها فى المشاركة السابقة
اسقاط r المجاور للزاوية يمثل المركبة z اى ان
اما الاسقاط المقابل للزاوية لا يمثل اى من المركبات x و y وانما هو الخط المظلل فى المستوى x-y ويساوى وهو يمثل نصف قطر جديد يمكن ان نسقطه فى اتجاه كل من x و y وعليه يكون اسقاط نصف القطر الجديد فى الاتجاه المجاور لزاوية هو المركبة x اى ان
اما اسقاط نصف القطر الجديد فى الاتجاه المقابل لزاوية يمثل المركبة y اى ان
وهكذا نحصل على معادلات التحويل من الاحداثيات الكارتيزية الى الاحداثيات الكروية
لحساب التغير فى x و y و z نجد ان x و y و z دوال فى كل من r و سيتا وفاى وعليه بتطبيق قاعدة السلسلة لثلاثة متغيرات نحصل على التغيرات التالية
ومن المعادلات (31) يمكن مباشرة حساب التفاضلات التى تظهر فى المعادلة الاخيرة
وبتعويض هذه التفاضلات فى المعادلات (32) نحصل على
وهكذا نستطيع حساب مربع عنصر الطول فى الاحداثيات الكروية على النحو التالى
و بعد فك الحدود المربعة فى المعادلة اعلاه واستخدام العلاقة المثلثية التى ورد ذكره فى المشاركة السابقة سوف نحصل على
وبمقارنة هذه المعادلة مع الصيغة العامة التالية
نحصل على قيم المعاملات والتى تمثل مركبات الممتد المترى فى نظام الاحداثيات الكروية
وجميع بقية مركبات g تساوى الصفر
يمكن ترتيب مركبات g فى شكل مصفوفة على النحو التالى :
وهذا هو الممتد المترى فى نظام الاحداثيات الكروى
لقد تحدثنا فى المشاركتين السابقتين عن تحويل نظام الاحدثيات من الاحداثيات الكارتيزية الى الاحداثيات القطبية و الاحداثيات الكروية , ولكن لم نتحدث عن ادخال البعد الزمنى كمحور وكانت مناقشتنا تنحصر فى انوع محددة من نظم الاسناد, الان نريد ايجاد صيغة عامة للتحويل من اى نظام احداثيات رباعية الى اخر . ومن جل هذا سوف نعمم نفس الطريقة التى استخدمناها فى المشاركة السابقة :
الطريقة العامة لتحويل نظم الاحداثيات
1) نعرف نظام احاثيات رباعى 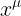 مركباته هى
مركباته هى 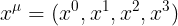 وسوف نفترض انها تعتمد على معامل واحد هو s اى انها جميعها دوال فى s اى
وسوف نفترض انها تعتمد على معامل واحد هو s اى انها جميعها دوال فى s اى 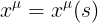
2) الان نريد التحويل من نظام الاحداثيات العام 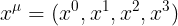 الى نظام احداثيات عام اخر هو
الى نظام احداثيات عام اخر هو 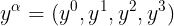
3) لاحظ انه ليست لدينا اى فكرة عن العلاقة بين النظامين الاحداثين x و y كما كانت لدينا العلاقات التى تربط الاحداثيات الكارتيزية بالاحداثيات الكروية فى المعادلات (31) ولكن كل ما نعلمه هو وجود علاقة ما تربط 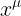 ب
ب 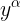
اى ان نظام الاحداثيات الجديد دالة فى نظام الاحداثيات القديم
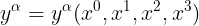
4) نستخدم قاعدة السلسلة لايجاد التغير فى نظام الاحداثيات y (مثلما فعلنا فى المعادلات (32))
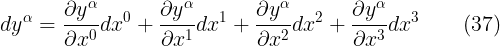
والمعادلة الاخيرة يمكن كتابتها فى شكل مجموع كما يلى
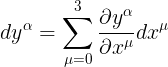
يمكن للقارئ ان يستخدم قاعدة تجميع انشتاين ويسقط لامة التجميع طالما ان المعامل ميو قد تكرر مرتين فى المعادلة
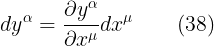
لا حظ ان المعامل التفاضلى 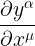 به معاملين الفا و ميو (لترغيم الصف والعمود) لذا يلعب دور مصفوفة غير شاذة (محددها لا يساوى الصفر)
به معاملين الفا و ميو (لترغيم الصف والعمود) لذا يلعب دور مصفوفة غير شاذة (محددها لا يساوى الصفر)
الان ايضا من المعادلة الاخيرة يمكن ايجاد التحويل العكسى من نظام الاحداثيات y الى نظام الاحداثيات x اى ان
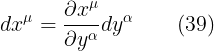
وهذا هو التغير فى الاحداثى  اما التغير فى احداثى
اما التغير فى احداثى  فهو يعطى بنفس المعادلة اعلاه فقط بتغير ميو الى نيو وتغير الحرف المتكرر باى حرف اخر (كما يحلو للقارئ فله مطلق الحرية فى اختيار الحرف المتكرر) وليكن بيتا مثلا
فهو يعطى بنفس المعادلة اعلاه فقط بتغير ميو الى نيو وتغير الحرف المتكرر باى حرف اخر (كما يحلو للقارئ فله مطلق الحرية فى اختيار الحرف المتكرر) وليكن بيتا مثلا
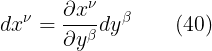
الان بضرب المعادلتين (39) و (40) نحصل على
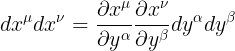
اذا ضربنا طرفى المعادلة الاخيرة فى الممتدد المترى فى منظومة الاحداثيات x نحصل على مربع طول الفترة
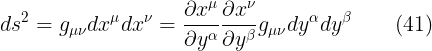
اذن من الواضح ان الحد المضروب فى 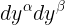 فى الطرف الايمن من المعادلة الاخيرة, هو الممتدد المترى فى نظام الاحداثيات y والذى سوف نرمز له برمز g تيلدا
فى الطرف الايمن من المعادلة الاخيرة, هو الممتدد المترى فى نظام الاحداثيات y والذى سوف نرمز له برمز g تيلدا
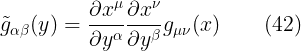
وهكذا نكون قد تحصلنا على الطريقة العامة لتغير نظام الاحداثيات و المعادلة (42) هى المعادلة العامة لتغير الممتدد المترى من اطار الى اخر
معادلة الجيودسك

الجيودسك هو اقصر خط يربط بين نقطتين فى الفضاء المنحنى. لا يجاد هذه المعادلة سوف نستخدم النتائج التى تحصلنا عليها فى المشاركة السابقة وهى حرية تغير نظام الاحداثيات كيفما نشاء طالما ننا نطبق قوانين التحويل سالقة الذكر.
من اجل التبسيط افترض ان نظام الاحداثيات 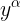 هو نظام كارتيزى (مستوى) اما النظام
هو نظام كارتيزى (مستوى) اما النظام 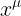 هو عبارة عن فضاء منحنى, وهكذا طالما ان نظام الاحداثيات
هو عبارة عن فضاء منحنى, وهكذا طالما ان نظام الاحداثيات 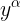 هو نظام مستوى, فان اقصر خط يربط بين نقطتين هو الخط المستقيم , اما نظام الاحداثيات x فهو نظام احداثيات لفضاء منحنى لذا فان اقصر خط فيه هو ما يعرف بالجيودسك
هو نظام مستوى, فان اقصر خط يربط بين نقطتين هو الخط المستقيم , اما نظام الاحداثيات x فهو نظام احداثيات لفضاء منحنى لذا فان اقصر خط فيه هو ما يعرف بالجيودسك
دعنا الان نحسب معدل تغير 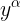 بالنسبة لمعامل s (بالطبع تفاضل الخط المستقيم يمثل ميل الخط المستقيم) ولكن نحن افترضنا ان نظام الاحداثيات
بالنسبة لمعامل s (بالطبع تفاضل الخط المستقيم يمثل ميل الخط المستقيم) ولكن نحن افترضنا ان نظام الاحداثيات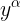 يعتمد على
يعتمد على 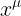 لذا سوف نستخدم قاعدة التفاضل الضمنى( او قاعدة السلسلة )
لذا سوف نستخدم قاعدة التفاضل الضمنى( او قاعدة السلسلة )
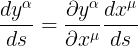
لاحظ ان تكرر المعامل الحر ميو يستلزم عملية الجمع (قاعدة انشتاين للتجميع)
الان نريد حساب المشتقة الثانية 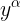 (اى تفاضل المشتقة الاولى وهو يساوى تفاضل الميل الثابت للخط المستقيم)
(اى تفاضل المشتقة الاولى وهو يساوى تفاضل الميل الثابت للخط المستقيم)
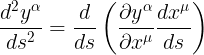
لاحظ ان التفاضل فى الطرف الايمن من المعادلة الاخيرة هو تفاضل حاصل ضرب دالتين ويخضع للعلاقة
( الدالة الاولى فى تفاضل الدالة الثانية زائدا تفاضل الدالة الاولى فى الدالة الثانية)
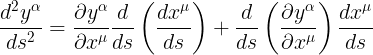
لاحظ ان الحد الثانى فى المعادلة الاخيرة هو تفاضل بالنسبة ل s لمقدار يعتمد ضمنيا على s لذا يجب تطبيق قاعدة التفاضل الضمنى مرة اخرى على هذا الحد لنحصل على
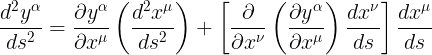
لاحظ وجود الجمع لتكرار المعامل ميو فى الحد الاو ل الايمن ووجود الجميع على ميو ونيو فى الحد الثانى فى الطرف الايمن. دعنا الان نغير المعامل المتكرر ميو فى الحد الاول الى معامل اخر لامدا وذلك لكى نتمكن كن استخراج عامل مشترك بين الطرفين من دون ان يظهر حرف ميو متكررا اكثر من مرة واحدة فى الحد الثانى (تزكر اننا قلنا ان للقارئ مطلق الحرية فى تسمية الحرف المترر ولكن يجب عدم تكرره اكثر من مرة لكى لاتلتبس عليه عملية الجمع)

باستخراج 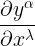 من طرفى المعادلة الاخيرة سوف يظهر مقلوبه (التفاضل العكسى) مضروبا فى الحد الثانى فى الايمن
من طرفى المعادلة الاخيرة سوف يظهر مقلوبه (التفاضل العكسى) مضروبا فى الحد الثانى فى الايمن

قلنا ان y عبارة عن فضاء مستوى لذا فان اقصر خط يربط بين نقطتين هو الخط المستقيم وعليه المشتقة الاولى بالنسبة ل s تمثل ميل الخط المستقيم (من الناحية الدينميكية فان المشتقة الاولى بالنسبة ل s مقسومة على سرعة الضوء تمثل السرعة اللحظية) اما المشتقة الثانية فهى عبارة عن تفاضل للميل الثابت للخط المستقيم وعليه يجب ان تساوى الصفر (المشتقة الثانية للسرعة تساوى التسارع ) وهكذا يكون الطرف الايسر من المعادلة الاخيرة مساويا للصفر والسبب هو
هندسيا: ميل الخط المستقيم فى الفضاء المستوى يكون ثابتا وعليه فان تفاضله يساوى الصفر
فيزيائيا : اذا استبدلنا s/c (اى زمن اطار السكون) فان المشتقة الاولى تمثل السرعة الثابتة اما المشتقة الثانية تمثل التسارع ولماكانت السرعة ثابته فان التسارع يجب ان يساوى الصفر
وهكذا بالتعويض فى المعادلة الاخيرة نحصل على معادلة الجيودسك وهى معادلة اقصر خط يربط بين نقطتين فى فضاء منحنى

الحد

يعرف بحد كرستوفل ويرمز له بالرمز 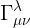 ولو لا هذا الحد (اى انه لا يساوى الصفر) لكانت المشتقة الثانية ل x تساوى صفرا وهذا واضح من المعادلة الاخيرة. اذن فان هذا الحد يدل على وجود انحناء (لا يساوى الانحناء ولكن يدل على الانحناء) فى نظام الاحداثيات x . اما اذا نظرنا له من الناحية الفيزيايئية فلو لا هذا الحد لكان التسارع يساوى الصفر وعليه فان هذا الحد يدل على وجود مصدر للتسارع اى يرتبط بالقوة التثاقلية
ولو لا هذا الحد (اى انه لا يساوى الصفر) لكانت المشتقة الثانية ل x تساوى صفرا وهذا واضح من المعادلة الاخيرة. اذن فان هذا الحد يدل على وجود انحناء (لا يساوى الانحناء ولكن يدل على الانحناء) فى نظام الاحداثيات x . اما اذا نظرنا له من الناحية الفيزيايئية فلو لا هذا الحد لكان التسارع يساوى الصفر وعليه فان هذا الحد يدل على وجود مصدر للتسارع اى يرتبط بالقوة التثاقلية
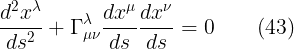
وهى المعادلة العامة للجيودسك وهى تمثل مسار الشعاع الضوئى فى الفضاء المنحنى لان الضوء يسلك اقصر مسار يربط بين نقطتين
لاحظ فى الرسم ادناه لو كان الفضاء مستويا لسلك الضو المسار الاحمر ولكن نسبة لان الفضاء منحنيا نسبة لوجود قوى تثاقل نجمت عن الكتلة المبينة بالرسم, فان الضوء يتحرك فى الجيودسك المبين باللون الازرق الفاتح

عامل كرسوفل Christoffel symbol
فى المشاركة السابقة اوجدنا عامل كرسوفل بدلالة التفاضلات على الاحداثيات المحلية و لكن بشكل عام يمكننا ان نكتب عامل كرسوفل بدلالة التفاضلات على الممتدد المترى على النحو التالى
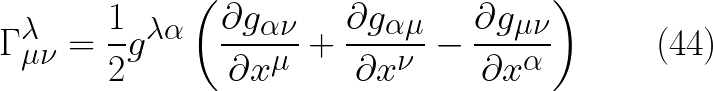
لاحط ان تكرار المعامل الفا يعنى الجمع من الفا=صفر الى الفا=3 وايضا يجب على القارئ ان ينتبه الى ان 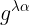 هو معكوس الممتدد المترى
هو معكوس الممتدد المترى 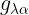
لاحظ ان من خواص عامل كرسوفل انه لا يتخير عند تغير ميو بنيو (فقط نكون بدلنا التفاضلين الاول والثانى فى المعادلة (44)) اى ان
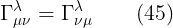
تمرين (1):
اوعطيت ان الممتدد المترى لفضاء زمنكانى رباعى الابعاد يعطى ب
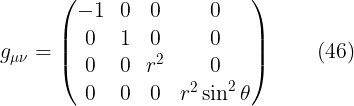
مستخدما المعادلة (44) والخاصية (45) احسب جميع مركبات عامل كرسوفل غير الصفرية
تلميح: المسألة تعتمد فقط على حساب التفاضلات والتعويض المباشر لحساب المركبات لعامل كرستوفل
تنوية: يستحيل على اى قارئ ان يتعلم النسبية العامة دون ان يحل مسائل وتمارين, وصدقونى سوف يتعلم القارئ الكثير من حل التمارين. مثلا المبتدئ لاول مرة سوف يحسب 64 حدا ليصل الى المركبات اعلاه اما اذا استخدم الملاحظة (45) سوف يحسب 40 حدا فقط وبالممارسة واستخدام الحدس الفيزيائى سوف يكون القارئ قادرا على اختيار مركبات محددة هى بالضبط الكميات غير الصفرية لعامل كرستوفل, وهذا لا يتاتى الا بحل مثل هذه التمارين.
اذا كنت جادا فى رغبتك فى تعلم النسبية العامة وقمت بحل هذا التمرين فضع حلك فى موضوع منفصل باسم حلول تمارين النسبية العامة واذا تحصلت على الاجابات الصحيحة سوف ننقل مشاركتك الى هذا الموضوع
 الرقابة الجبائية هي الوسيلة الضرورية لضمان المساواة بين الأفراد في دفع للضريبة . وتشكل شرطا من الشروط الأساسية والفعالة لتحقيق منافسة شريفة وعادلة بين المؤسسات [ ]
الرقابة الجبائية هي الوسيلة الضرورية لضمان المساواة بين الأفراد في دفع للضريبة . وتشكل شرطا من الشروط الأساسية والفعالة لتحقيق منافسة شريفة وعادلة بين المؤسسات [ ]