السلام عليكم احبائي
موضوعنا اليوم عن
هندسة البرمجيات
وبالنسبة لتصمبم الموضوع فاراكم مهمة جدا


أهلا بكم
اليوم جأتكم بموضوع قيم و رائع
و هو موضوع عبارة عن
الكميات العددية والكميات المتجهة
في المجال الفيزيائي
و الأن أترككم مع
الموضوع
أتمنى ان ينال إعجابكم
و شكرا

تقسم الكميات الفيزيائية الى نوعين :
1- الكميات العددية ( القياسية ) Scalar Quantities
وهذه الكميات التي يلزم لتعريفها مقدار ( رقم ) ووحدة فيزيائية . واحدى هذه الكميات هي : الحجم , الكتلة, الزمن , الشغل والطاقة .
فمثلاً نقول : حجم المخبار = 200 سم 3 , كتلة الكرة = 80 غم .
2- الكميات المتجه Vector Quantities .
وهي الكميات التى يلزم لتعريفها مقدار ووحدة فيزيائية واتجاه .
ولا يتم تعريفها الا اذا اكتملت هذه العناصر .
ومن الامثلة على الكميات المتجهة : السرعة , القوة , التسارع و الازاحة .
فمثلاً إذا قلنا تحركت سيارة بسرعة 60 كم/ ساعة فقط , فهذا لايتم المعنى , لأن تحركها قد يكون شمالاً أو جنوباً أو في أي اتجاه , وفي كل حالة تكون النتيجة مختلفه.
وللتعامل مع هذه الكميات يتم استخدام تمثيل رياضي يسهل على الدارس التعامل مع هذه الكميات
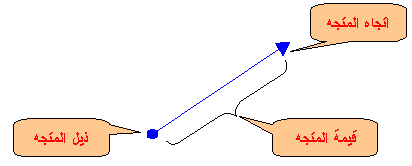
كل كمية فيزيائية متجهة يمكن تمثيلها بالمتجة ” vector ” المتجهة هو : ” تمثيل رياضي , يعبر عن الكمية الفيزيائية المتجهة مقداراً واتجاهاً وهو عبارة عن خط مستقيم في نهايته سهم , وطول الخط المستقيم يتناسب مع مقدار الكمية الفيزيائية في حين أن اتجاهه يدل على اتجاهها “.
 .
.
تحليل المتجهات :
إذا اخترنا محاور متعامدة وأسمينا المحور الأفقي س ، والمحور الرأسي ص . ثم رسمنا المتجهة السابق ( ق ) في المستوى بين س ، ص بدءاً من نقطة الأصل .
بحيث هذا المتجه يصنع زاوية مقدارها 45 ْ مع محور السينات الموجب , ولنسميها ( q )



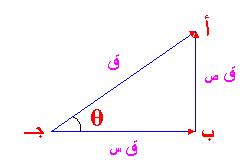
( أ جـ ) 2 = ( أ ب ) 2 + ( ب جـ ) 2
ق 2 = ( ق جا q ه) 2 = ( ق جا q ه) 2
ق 2 = ق 2 جا 2 q ه + ق 2 جتا 2 q ه
ق 2 = ق 2 ( جا 2 q ه + جتا 2 q ه )
ومن قانون المثلثات ( جا 2 q + جتا 2 q ه ) = 1
إذن ق 2 = ق 2 …. وهذا هو اثبات لنظرية فيثاغورس
والآن ق 2= ق 2 س + ق 2 ص
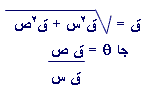
أ- طريقة الرسم :
تعتمد هذه الطريقه على أنه اذا نقلنا المتجه بحيث نحافظ على مقداره ويظل اتجاهه موازيا” للاتجاه الاصلي , فأننا نحصل على نفس المتجه .
ولجمع المتجهات بهذه الطريقه نصل المتجهات رأسياً الواحد بذيل الآخر , ويكون المجموع هو متجه يبدأ من ذيل المتجه الأول إلى رأس المتجه الأخير .
ويعبر عن الجمع بـ :
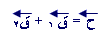
مثال 1 :
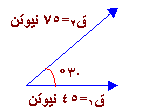
أوجد حاصل جمع المتجهين ق 1 ، ق 2
الحل :
1- نعيد الرسم وفق مقياس رسم مناسب كل 15 نيوتن يمثلها 1 سم على الرسم .
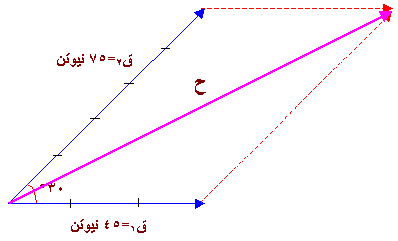
2- انقل ق 2 إلى اليمين ( حافظ على المقدار والاتجاه ) بحيث ينطبق ذيلها على رأس 
3- المجموع ( 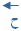 ) يكون المتجه من ذيل المتجه الأول إلى رأس المتجهة الأخير .
) يكون المتجه من ذيل المتجه الأول إلى رأس المتجهة الأخير .
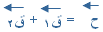
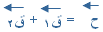
4- نقيس قيمة ( 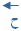 ) بالمسطرة
) بالمسطرة
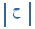 = 7.5 سم
= 7.5 سم
5- قيمة ( 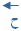 ) الحقيقية = 7.5 × 15 = 112.5 نيوتن .
) الحقيقية = 7.5 × 15 = 112.5 نيوتن .
في هذه الحالة :
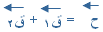
ويمكن القول أن :
ح س = ق 1س + ق 2س
ح ص = ق 1ص + ق 2ص
ولإيجاد المحصلة :

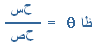
ويمكن القول أن :
ح س = ق 1س + ق 2 س
ح ص = ق 1 ص + ق 2 ص
مثال : يتحرك سائق رالي 36 كم باتجاه الشرق , ثم 42 كم باتجاه الشمال . أخيراً 25 كم باتجاه الشمال الغربي . حدد بعده عن نقطه البداية .
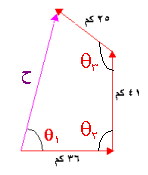 الحل :
الحل : نرسم رسم توضيحي للسؤال :
ح س = ف 1 جتا q ه 1 + ف 2 جتا q ه 2 + ف 3 جتا q ه 3
ح س = 36 + صفر + (25) ( جتا 135 ْ ) = (36 – صفر – 17.7 ) = 18.3 كم .
جا q ه 1 + ف 2 جا q ه 2 + ف 3 جا q ه 3 = ف 1 جا صفر + ف 2 جا 90 ْ + ف 3 جا 130 ْ = صفر + 42 + 17.7 = 59.7 كم .

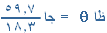
q =ه73 ْ
3- الضرب القياسي (العددي) Scalar Product
يعبر عن ( أ . ب ) ويرمز لهذا النوع من الضرب بـ ( . ) وينتج عنه كمية قياسية ( عددية ) ليس لها اتجاه بالرغم من أن الكميات في عملية الضرب هي متجهات .
مقدار حاصل الضرب = أ . ب جتا qحيث q الزاوية بين أ , ب ومن الأمثلة على هذا الضرب
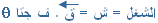
وتكون قيمة ( ش ) أكبر ما يمكن عندما تكون الزاوية q بين (ق ، ف) = صفر و تكون ش = صفر عندما تكون الزاوية بين ( ق ، ف ) = 90 ْ
4- الضرب الاتجاهي V ectar P roduct
يعبر عنه ( أ × ب ) ويُرمز لهذا النوع من الضرب بـ ( × ) وينتج عنه كمية متجهة .
وقيمة هذا المتجه تحدد بـ ( أ ب جا q ه ) حيث الزاوية بين أ ، ب . أما اتجاه الكمية فيحدد بقاعدة اليد اليمنى حيث يشير الإبهام إلى إحدى الكميات( الكمية الأولى ) والأصابع إلى الكمية الثانية . وبذلك يكون اتجاه حاصل الضرب عمودياً على راحة اليد للخارج .
ومن الأمثلة على هذا الضرب :
– القوة المغناطيسية المؤثرة في شحنه .
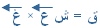
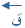 = 5 × 5 = 25 نيوتن شرقاً
= 5 × 5 = 25 نيوتن شرقاً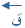
 تقبلوا خالص تحياتي و إحترامي
تقبلوا خالص تحياتي و إحترامي